Задачка для советских школьников из 1950-х собрала миллионы просмотров. Попробуйте и вы
Автор предлагает необычный метод.
Автор ютуб-канала «Этому не учат в школе» выложил советскую задачу 1950-х годов. По словам блогера, этот математический пример решали в СССР больше 70 лет назад. В этой задаче нужно найти сумму шести дробей – (1/20) + (1/30) + (1/42) + (1/56) + (1/72) + (1/90) = ?
Математик заявил, что обычно для решения ищут общий знаменатель, но предложил другой способ. Он разложил нижние части дроби на множители – 20 на 4 и 5, 30 на 5 и 6, 42 на 6 и 7 и так далее.
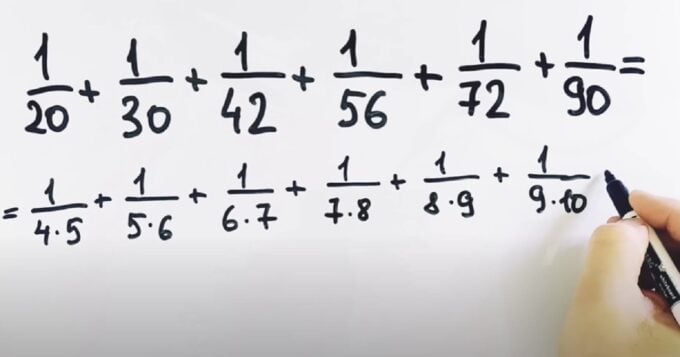
Затем автор обратил внимание, что единицу в числителе можно представить как разность тех же цифр, что и в знаменателе. Пример визуально еще больше усложнился, но блогер на этом не остановился и разбил цифры в числителе на отдельные дроби. Задача выросла на доске еще сильнее.
Лишь на этом этапе математик приступил к сокращению дробей. Он выкинул повторяющиеся цифры и получил такой результат: (115/4) – (112/10) = (5-2/20) = ?. В итоге конечный правильный ответ – 3/20.
За почти 1,5 года эта задача на ютубе набрала больше 2 миллионов просмотров. Но в комментариях автору указывают на искусственность задачи – при других знаменателях такой метод просто не сработал бы.
Комментарии